Being Inside a Perfectly Reflecting Sphere Or Torus

Version 1.0 of 1/6/2006-12:00 a.m.

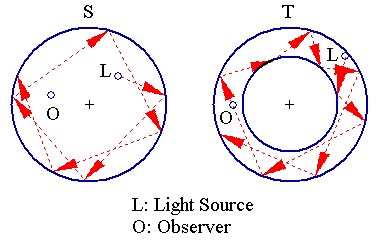
reflecting sphere/torus resonators

On 31/10/2005, the author posted this problem to sci.optics and sci.physics. The problem is described in more detail below.

Consider the following optical structures:

  1. A void sphere S with totally reflecting inner walls.
  2. A void torus T with totally reflecting inner walls.
  3. A (point or extended) light source L inside S and T.
  4. An observer O inside S and T.

Here are some interesting questions for you to ponder about:

  1. What would O see when O tries to look at the walls of S or T at various angles, while L is illuminating the inside of S or T?[1]
  2. What will O see when O tries to look at the walls of S or T at various angles, when either O or L move relative to the walls of S or T, while O is observing?[1]
  3. What happens to a single light ray which emanates from L inside S and T?
  4. Will any light ray emanating from L, eventually reach O in S and T?
  5. Will O be able to see L's reflection anywhere in S or T? Everywhere? Nowhere?
  6. Will O be able to see O's reflection anywhere in S or T? Everywhere? Nowhere?
  7. Will O be able to see L's reflection, even when L is hidden from O in T?
  8. What will O see in S or T, if L is a strobo flash which lights exactly once?
  9. Can S and T's of reasonable sizes (with radii 10-20 m) be built?
  10. Do you think they would be "safe" for human observers?
  11. Justify your answer about their "safety".
  12. How might S and T be related to "cavity resonators"?
  13. Assume S or T is built, without O/L in it. What will happen if one opens a little hole on the wall of S or T for some light to get in?
  14. Same question as above with O already in S or T.
  15. Can you perhaps think of a useful application of S and T in Physics?
  16. Would you volunteer to be O in experiments with S and T?
  17. Why/Why not?

A Short Analysis

The central problem above is the general case of what happens in two dimensions, which was a question posed by Costas Vlachos on sci.math:

Suppose a user shines a beam of light (say a laser) inside a perfectly reflective unit circle. Which points will be visited by the light ray and which will not?

Let us define the problem geometrically: Consider the unit circle and a user A who "shines" a laser at an angle θ from the tangent at A. Clearly we have:

ρ+2*φ=π,

θ+φ=π/2, =>
ρ=2*θ

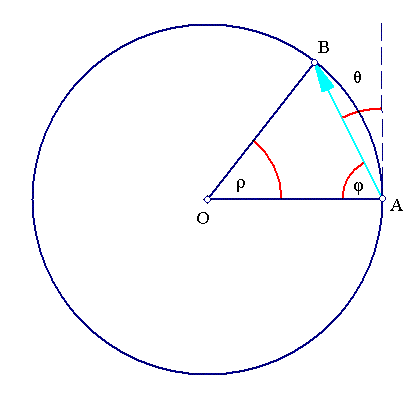
light ray in reflecting circle
User A shining a laser at angle θ inside the unit circle

Immediately then, when θ=π/n, n in N, ρ=2*π/n, and the resulting path will be a regular polygon with n sides. Therefore the visited points are exactly the n-th roots of unity: zn=1, or explicitly the points e2*k*π/n*i, k in {0,1,2,...,n-1}.

What about points which cannot be visited? These are the points z on the unit circle which do not satisfy zn=1, or the points e2*ρ*π*i, with ρ in R\Q.

Because ρ is also the central angle, these points are the points whose central angle ρ is not a rational multiple of 2*π. In other words, they are the points whose central angle ρ is an irrational multiple of 2*π.

The n-th roots of unity are dense on the unit circle, hence for any non-visited point subtending an (irrational) angle ρ, there exists n1, n2 in N, and consequently θ1, θ2, such that for any ε>0, we have |θ1-θ2|=π*|1/n1-1/n2|<ε, and that there exist points p1 on the path of shooting angle θ1 and p2 on the path of shooting angle θ2, such that: angle(p1) < ρ < angle(p2).

In other words, we can come as close as we want to the non-visited (irrational) points, by choosing appropriate angles θ1 and θ2.

Are the angles θ=π/n the only angles which give n-th roots of unity? On sci.math someone observed that the angle θ can be of the form θ=k/n*π, k in {0,1,2,...,n-1} and made the following conjecture:

For any ρ=m/n*2*π where m and n are relatively prime the light ray will trace out the endpoints of a regular n sided polygon, though not necessarily in the correct order.

The conjecture then can be reformulated in terms of θ as:

For any θ=k/n*π the light ray will trace out the endpoints of a regular n/GCD(k,n) sided polygon, though not necessarily in the correct order.

Indeed, the n-th roots of unity form a cyclic group of order n and the elements of this group of order k with GCD(k,n)=1 are generators. The situation is depicted on the following figure for n=6:

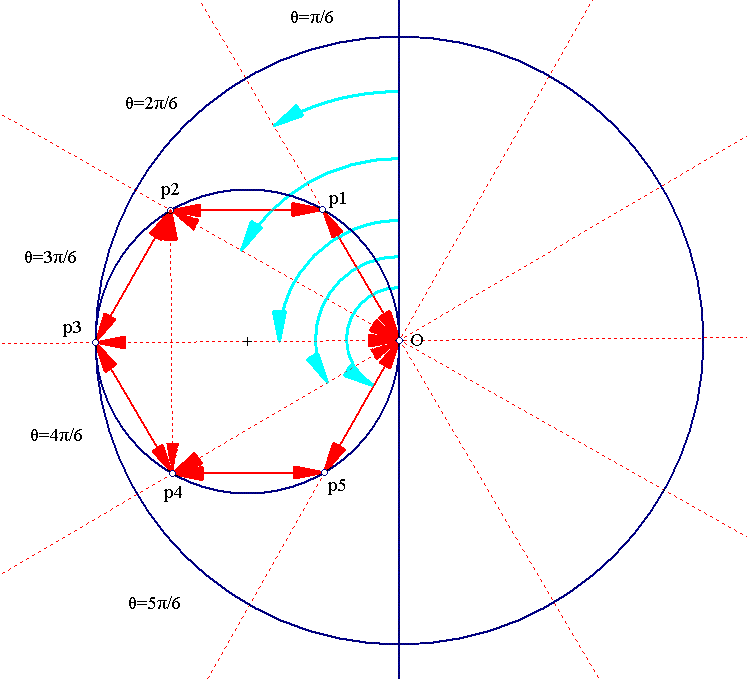
cyclic group of order 6

The paths traced according to the shooting angle θ are:

  1. n=6, k=1, θ=π/6, period: 6/GCD(1,6)=6, orbit: O-p1-p2-p3-p4-p5-O, hexagon
  2. n=6, k=2, θ=2*π/6, period: 6/GCD(2,6)=3, orbit: O-p2-p4-O, triangle
  3. n=6, k=3, θ=3*π/6, period: 6/GCD(3,6)=2, orbit: O-p3-O, line
  4. n=6, k=4, θ=4*π/6, period: 6/GCD(4,6)=3, orbit: O-p4-p2-O, triangle (in reverse)
  5. n=6, k=5, θ=5*π/6, period: 6/GCD(5,6)=6, orbit: O-p5-p4-p3-p2-p1-O, hexagon (in reverse)

The cases 2,3 and 4 exhibit subgroups of the cyclic group of order 6 formed by the second, third and fourth elements.

An Unexpected Connection With Infinite Exponentials

When considering the orbit of the sequence {z,cz,ccz,...} for various c in C, it turns out that the unit circle is exactly the boundary which separates the convergent sequences from the divergent ones.

Consider the map: φ:C -> C, defined by: φ(t)=et/et. φ is invertible. Specifically, φ-1(c)=-W(-log(c)), where W is Lambert's function.

When t=φ-1(c) and |t|<1, i.e., when t falls inside the unit circle, the sequence {z,cz,ccz,...} converges. When |t|>1, i.e., when t falls outside the unit circle, the sequence diverges.

When t is ON the unit circle, things are very interesting.

Specifically, when tk=φ-1(c) is an n-th root of unity (i.e., when tk=e2*k*π/n*i, k in {0,1,2,...,n-1}), the sequence {z,cz,ccz,...} converges when z=etk or falls into periodic cycling of period p=n/GCD(n,k) when z =/= etk.

When the sequence falls into periodic cycling, the orbit trajectory traces various (irregular) polygons, similar to the polygons on the light-mirror problem. Here is the orbit of the above sequence for tk=e2*k*π/6*i, i.e., for n=6 and k in {1,2,...,5}, with z perturbed -1/2 away from etk.

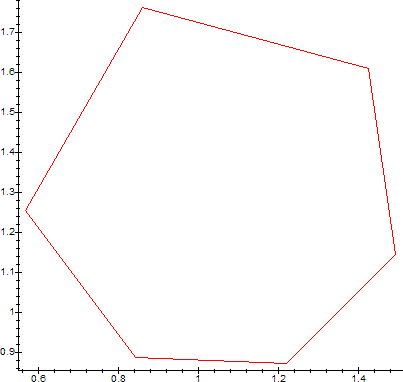
iterated exponential orbit 1
n=6, k=1, period: 6/GCD(1,6)=6, orbit: hexagon

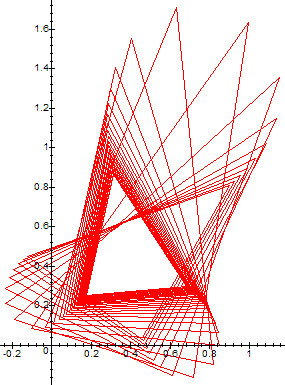
iterated exponential orbit 2
n=6, k=2, period: 6/GCD(2,6)=3, orbit: triangle

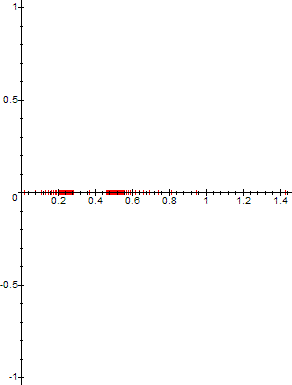
iterated exponential orbit 3
n=6, k=3, period: 6/GCD(3,6)=2, orbit: line

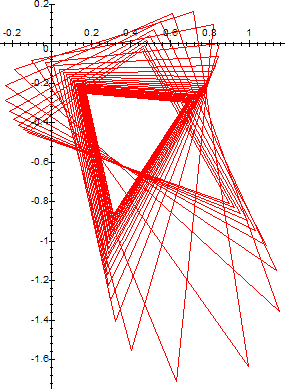
iterated exponential orbit 4
n=6, k=4, period: 6/GCD(4,6)=3, orbit: triangle (in reverse)

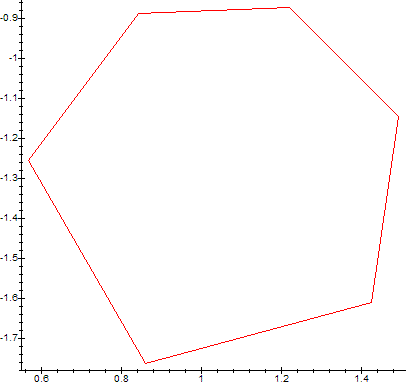
iterated exponential orbit 5
n=6, k=5, period: 6/GCD(5,6)=6, orbit: hexagon (in reverse)

What happens to points for which |t|=1, but t=φ-1(c) is NOT an n-th root of unity? These points correspond to the points which subtend a central angle ρ which is an irrational multiple of 2*π on the problem with the light-mirror trajectory. In this case, the sequence {z,cz,ccz,...} diverges (chaotically)[2].

Notes/References

  1. Brian Vanderkolk investigates the general case optically using POVRay, on this page. Brian's videos have been used by the author to simulate Reincarnation In Indra's Net of Pearls.
  2. For more info on this problem and on iterated exponential powers, consult the pages on Infinite Exponentials and A Slightly Deeper Analysis of Infinite Exponentials.