(The analysis that follows is a light introduction. For more austere results, consult Paper 1).
Having seen some clues about the behavior of zzz... for complex z, in the fractal in the previous section, it would be nice to investigate it a bit further. In fact, quoting a reference by John Bailey and Dave L. Renfro, which was posted in sci.math:
Baker and Rippon, "Convergence of infinite exponentials" Ann Acad Sci Fenn Ser AI Math 1983 179-186 showed that zzz... converges for log(z) contained in {t*e-t: |t| < 1 or tn = 1 for some n= 1, 2, ..} and that it diverges[1] elsewhere.
Let's look at it closer:
Assume that Log(z) is the principal branch of the complex log(z) in all the following steps.
Let also W denote the principal branch of the Lambert's W function.
Then:
It would be wiser to examine the behavior of the function f(z)=cz, instead of looking at the exponential through recursive sequences as I had done above.
First, we need a second Lemma:
Lemma #2:
if z is such that: Re(z)>-Im(z)*cot(Im(z)) and |Im(z)|<Pi, then W(z*ez)=z
We have good reason to believe this. In fact, Maple says:
>series(W(z*exp(z)), z, 7);
= z + O(z^7).
(It is tempting here to want to claim that W(z*ez)=z for ALL values of z. Unfortunately, this is NOT true. We will see later down why).
Proof:
From the definition of Lambert's W function:
W(z)*eW(z)=z
Here we are tempted to say:
using z=W-1(w) we get: (15)
W(W-1(w))*eW(W(-1)(w))=W-1(w),
so:
w*ew=W-1(w)
and therefore:
W(w*ew)=W(W-1(w)) = w.
But we have to be careful with step (15). Since W has a branch cut on real values of z in: (-oo,-1/e], we need to examine the behavior of the inverse: z*ez on those values a bit more carefully.
First let's look at the graph of f(z)=z:
>complexplot3d(z,z=-1-I..1+I);
Now let us see if the function W(z*ez) has any branch cuts. Indeed it does:
>h:=z->W(z*exp(z));
>complexplot3d(h(z),z=-1-I..1+I);
Here is the same function in more detail and different angles:
It is obvious that something strange happens at a well defined boundary of the W(z*ez) and outside this boundary the function differs radically from the function f(z)=z, so we need to investigate this boundary a bit further.
Since W has a branch cut on real values of z in (-oo, -1/e], we expect this branch cut to give rise to new branch cuts for W(z*ez). And indeed it does. The new branch cuts will come precisely from those values of z, for which z*ez (W's inverse) is in (-oo,-1/e].
Those values then, will be those for which:
z*ez=w is in (-oo,-1/e]
But the solution to the above equation is none other (by the definition of W!!) than:
z=W(w) with w in (-oo,-1/e].
Since W's branch cut starts at -1/e, we can force w to range in (-oo,-1/e] and see what happens to the image:
>complexplot(W(w),w=-exp(-1)..-10);
The curve above defines a branch cut for all such z with Arg(z) in [0, Pi]. Another branch cut for the function W(z*ez) is defined for those z with Arg(z) in [Pi, 2*Pi].
And the surprise here is that the two cuts are none other than the curve -y*cot(y)+y*I, which is the image of (-oo,-1/e] under the LambertW! The figure below is the graph of this curve, but not to scale.
Do we indeed have a branch cut at -y*cot(y)+y*I? Let's try to see this since we have bothered with it so far:
Note that if k>0 then
W(z*ez) is close to -y*cot(y)+y*I, if
z*ez is close to -1/e-k+/-epsilon*I,
which happens if:
z is close to W(-1/e-k+/-epsilon*I).
First we need a third Lemma:
conjugate(W(z))=W(conjugate(z));
Proof:
This is one of the standard properties of Lambert's W function and is contained in a paper by Corless which describes the function in detail.
Now, let w be a real number in the range (-oo,-1/e] and let z1 and
z2 be:
z1=W(w+epsilon*I),
z2=W(w-epsilon*I).
Now by the definition of W:
z1*exp(z1)=w+epsilon*I, and
z2*exp(z2)=w-epsilon*I.
Now if f(z)= W(z*ez),
|f(z1)-f(z2)|=|W(z1*exp(z1))-W(z2*exp(z2))| (16)
Since z2 falls inside the -y*cot(y)+y*I curve,
W(z2*exp(z2))=z2 by Lemma #2, and
W(z1*exp(z1))=
W(w+epsilon*I)=
W(conjugate(w-epsilon*I))=
conjugate(W(w-epsilon*I))=
conjugate(z2), using Lemma #2 and #3.
So (16) becomes:
|conjugate(z2)-z2| >=
2*Im(z2) = constant.
So indeed, the curve -y*cot(y)+y*I defines a branch cut. Let us verify this, using some Maple code:
> f:=z->W(z*exp(z));
> epsilon:=0.001;
> k:=13; #set any appropriate positive k
here.
> z1:=W(-exp(-1)-k+epsilon*I);
> z2:=W(-exp(-1)-k-epsilon*I);
> evalf(f(z1));
> evalf(f(z2));
> evalf(abs(f(z2)-f(z1)));
> evalf(2*Im(z2));
and indeed, |f(z1)-f(z2)|>=2*Im(z2).
To conclude:
if z is inside the curve, then W(z*ez)=z,
in other words: if z is such that: Re(z)>-Im(z)*cot(Im(z)) and |Im(z)|<Pi, then W(z*ez)=z.
The restriction |Im(z)|<Pi, ensures that z is inside the MAIN region (that which includes the origin) that is defined by the curve -y*cot(y)+y*I. The condition Re(z)>-Im(z)*cot(Im(z)) is satisfied by other z's as well that fall outside this region. I haven't checked the validity of the lemma for those z's, but it appears that it is false for those z's. In any case, we don't care, since we need the lemma for the unit disk only. See below. The value Pi for the restriction comes from the fact that the curve -y*cot(y)+y*I has two asymptotes, at +/-Pi.
Now, we can go back to the proof of Lemma #2 and complete it.
(Note that an immediate side consequence of the proof for the lemma is that if z is such that: Re(z)>-Im(z)*cot(Im(z)) and |Im(z)|<Pi then W-1(w)=w*ew).
Continuing with the rest of the proof:
We now iterate the function:
f(z)=cz
Our fixed points z are given by:
-W(-Log(c))/Log(c), (2)
then, using the part of the hypothesis that Log(c)=t*e-t, (2) becomes:
W(-t*e-t)/(-t*e-t) (3)
Using the second Lemma: W(-t*e-t)=-t, when t is inside the unit circle, since the unit circle falls INSIDE the curve that defines the branch cut (-y*cot(y)+y*I) (below),
(3) then becomes:
=-t/(-t*e-t)
=et.
Iterating the function f(z) at its fixed point et, we get:
[e(t/et)][e(t/et)][e(t/et)]...=et.
It is interesting to note that the fixed points et are indeed attractors:
if c0 is a fixed point of f(z), c0 it is an attractor, if:
|f'(c0)|<1 (4)
Using the hypothesis:
|f'(c0)|
=|t*e-t*eLog(c)*et|
=|t*e-t*et*e(-t)*et|
=|t*e-t*et|
=|t|<1
which is true in view of the hypothesis. Convergence follows from a theorem by Shell:
Theorem (Shell): cc... converges to et in some neighborhood of et if |t|<1 and can do so only if |t|<=1.
Now let tk=e2*k*Pi/n*i be a complex n-th root of unity,
with k in {0,1,2,...n-1}.
Using c=eLog(c),
and since Log(c)=t*e-t from the hypothesis,
consider the functions fk(z)=ckz, where ck=e(tk/etk)
The fixed points for the functions fk(z) are again calculated through the expression -W(-Log(ck))/Log(ck):
zk=-W(-Log(ck))/Log(ck)
-W(-tk*e-tk)/(tk*e-tk) (5)
Now, tk is a complex n-th root of unity, thus it is ON the unit
circle, so:
W(-tk*e-tk)=-tk, from Lemma #2, so (5)
becomes:
-tk/(-tk*e-tk)
=etk
Then, it is immediately obvious, that the points zk= etk
are fixed points for their corresponding functions, fk(z).
Iterating the functions fk(z) at their corresponding fixed points zk,
and using a similar analysis to that above, we get:
[e(tk/etk)][e(tk/etk)][e(tk/etk)]...=etk.
A couple of observations:
It is interesting to note that the fixed point condition (4), fails badly with the case 2: tn=1,
since if we attempt to use it (using etk as the fixed points on the derivative of fk(z)), we get:
|fk'(etk)|=
=|Log(ck)*cketk|
=|tk*e-tk*etk|
=|tk|
=1, since all the n-th roots tk lie on the unit circle.
(Actually the fact that it fails is a good indicator that the fixed points are quite "sensitive", most likely unstable)
After looking at the corresponding fractal above (the one with the double bulb near the origin) it becomes apparent that the case tn=1 concerns the periphery of the double bulb itself. In fact, the n roots of unity, get mapped onto the periphery of the bulb, under the map h(z)=ez*e-z.
Here is some Maple code to verify this:
First, the roots themselves:
>restart;
>with(plots):
>t:=(k,n)->exp(2*k*Pi*I/n);
>UR:=[evalf(seq( [Re(t(k,60)),Im(t(k,60))], k=0..59 ))]:
>plot(UR,style=point);
And then, the roots under the appropriate transformation:
>h:=z->exp(z*exp(-z));
>URT:=[evalf(seq([Re(h(t(k,60))),Im(h(t(k,60)))], k=0..59 ))]:
>plot(URT,style=point);
In particular, -1 gets mapped onto (1/e)e and 1 gets mapped onto e1/e. That's why the real range of the double bulb IS exactly, [(1/e)e,e1/e]
Note also that the fixed points etk of the functions fk(z) are unstable.
If we perturb z away from etk, the iterates of the function f(z)=cz will eventually form a p-cycle where p depends on k and n. (The results here can be very deep, as number theory enters the game...)
That is, the sequence {z, cz, ccz, ...} will eventually stabilize onto the p-cycle: {c0, fk(c0), fk(2)(c0), ...fk(p-1)(c0)}, where c0 is a solution to the equation: "fk(p)(z)=z" (p total c's).
(Note that there exist solutions to fk(p)(z)=z, distinct from the trivial one: W(-Log(c))/(-Log(z))), but Maple cannot find them since it can only solve the equation: f(n)(z)=z, for n=1, but not for any n>1. To see these solutions, consult the article on Solving the Second Real Auxiliary Equation)
p, as stated, depends on both k and n and now GCD's and other nice number theoretical goodies enter the game.
As above, ck= etk is a fixed point of f(n)(z), for all n. (since it is a fixed point of f(1)(z)=f(z))
To try to see the behavior of f around those known fixed points etk, we define:
f(1)(z)=cz, as above, and
f(n)(z)=f(f(n-1)(z)),
and look at |[f(p)(c0)]'|.
On the other hand, it can be shown by induction that:
[f(n)(z)]'=[Log(c)]n*Prod(f(k)(z), k=1..n), so:
|[f(p)(etk)]'|
=|Log(ck)p*(etk)p|
=|[Log(ck)*etk]p|, but this is:
|[tk/etk*etk]p|
=|tkp|
=1,
and this stubbornly refuses to give us any information.
However the above actually gives us a small clue about what happens on the
boundary:
|tn|=1 => {|t|=1 and tn=1 OR |t|=1 and tn
<>1, n in N}
Here is some Maple code to actually view the cycles. The code constructs the corresponding functions fk and iterates them (perturbed slightly) at their fixed points etk. (Set n and k to desired values).
> t:=(k,n)->exp(2*k*Pi/n*I);
>n:=5;
>for k from 0 to n-1 do
>c[k]:=exp(t(k,n)*exp(-t(k,n))); #calculate the corresponding c_k's
>od:
>for k from 0 to n-1 do
>f[k]:=z->c[k]^z; #calculate the corresponding f_k's
>od:
>perturb:=3.5; #purturb a bit
>for k from 0 to n-1 do
>z[k]:=exp(t(k,n))+perturb; #calculate some points close to the fixed points
>od:
>k:=2; #set for iterations with specific k
> rLim:=evalf(Re(exp(t(k,n))));
> iLim:=evalf(Im(exp(t(k,n)))); # calculate actual limit point
> URL:=[[rLim,iLim]]: #graph of limit point
>UR:=[evalf(seq([Re((f[k]@@m)(z[k])),Im((f[k]@@m)(z[k]))], m=1..50 ))]:
>plot({UR,URL},-1..1,-1..1,style=point,color=red);
Here is the cycle along with the limit point for the third 5-th root of unity (k=2, n=5), perturbed 3.5 away from the limit point:
And here is the cycle trajectory:
(An interesting connection exists between those trajectories above and a certain optics problem. For details, check this page).
An Example of Chaos
Use exactly the same Maple code as above, but replace the line:
> t:=(k,n)->exp(2*k*Pi/n*I);
with:
> t:=(k,n)->exp(2*sqrt(2)*Pi*I); #an irrational multiple of 2*π
Result:
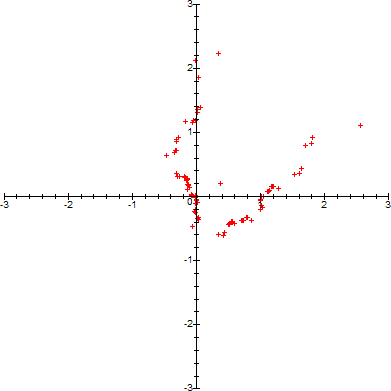
(The resultant chaotic turbulence of the orbit is directly proportional to the magnitude of the "perturb" factor).
On the other hand, let K={z: Log(z)=t*e-t, |t| <=1} be the main kidney-shaped region along with its boundary on the figure above and let c not in K.
e-W(-Log(c))/(e-W(-Log(c)))
=e-W(-Log(c))/(W(-Log(c))/(-Log(c)))
=eLog(c)
=c
so t=-W(-Log(c)) is a pre-image of the point c, under the map h(z)=ez*e-z. Necessarily then:
|t|=|W(-Log(c))|> 1 (16)
for otherwise, h(t)=c in K and this is not the case by assumption.
Since f(z)'s fixed points c0 are always given by -W(-Log(c))/Log(c):
|f '(c0)|
=|Log(c)*cc0|
=|Log(c)*e-W(-Log(c))|
=|Log(c)*W(-Log(c))/(-Log(c))|
=|W(-Log(c))|>1 (17)
using (16). But the later implies that f(n)(z), n in N, c not in K cannot possibly converge to a limit l, for if it did, f(l)=l and |f'(l)| <= 1, contradicting (17).