| Absolutely certain | Obvious | Less certain | Less... | ... | Chaos |
| r(S)=1 | r(S)=0.8 | r(S)=0.6 | r(S)=0.3 | ... | r(S)=0 |
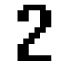 |
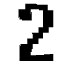 |
 |
 |
... |  |
 |
 |
 |
 |
... |  |
Intelligence appears to depend highly on recognizing patterns. Here the author attempts a qualitative and quantitative (pseudo-)analysis of how intelligence can be used to understand pattern recognition, based on some simple ideas.
The author begins with some assumptions/definitions.
The author defines the recognizability of symbol S, r(S), to be such that 0≤r(S)≤1, with r(S)=1 denoting absolute certainty for the existence of at least one underlying pattern in S and r(S)=0 denoting absolute certainty for the lack of existence of any underlying patterns in S.
Clearly, there is a huge variation of r(S) for various S's. Two values are of immediate interest: 0 and 1. 1 represents absolute recognizability and 0 represents absolute non-recognizability. Values in between represent various levels of recognizability, and the transitions may be discrete or continuous depending on intelligence.
The author shows an example of symbol manipulation for two symbols, the fundamental symbol for the number 2, and a very complex symbol which is used to attract consumers. The two symbols have been distorted in Photoshop using the Distort->Glass... filter, to illustrate the various values of r(S). The last image has been gotten by applying the same filter a large number of times.
| Absolutely certain | Obvious | Less certain | Less... | ... | Chaos |
| r(S)=1 | r(S)=0.8 | r(S)=0.6 | r(S)=0.3 | ... | r(S)=0 |
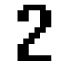 |
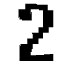 |
 |
 |
... |  |
 |
 |
 |
 |
... |  |
A sub-symbol Sn in S, is a recognizable pattern which is a subset of S (for example, the letter "C" (the first letter of the world "CAMEL"), is a sub-symbol of the Camel pack symbol). The author next defines the depth of symbol S, D(S), as follows:
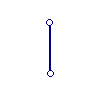
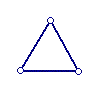
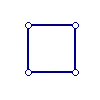
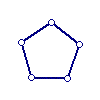
The above recursion is a bit vague. Note however that letters can be made fundamental, by mapping them to the Naturals. Geometric shapes can also be made fundamental using the following correspondence:
| 0 | 1 | 2 | 3 | 4 | 5 | ... |
 |
 |
 |
 |
 |
 |
... |
One hopes that heuristically the recursion will eventually bottom out, so let's try to evaluate D(S), for S being the following image:
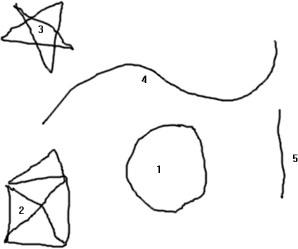
Relatively simple compound symbol S
All the sub-symbols (5) are not geometric but are still all recognizable, hence 0<r(S)<1. Indexing the sub-symbols as in the figure, D(1)=0, D(2)≥16 (why?), D(3)≥13, D(4)=1, D(5)=1, hence D(S)≥31. S's depth is high, but still pretty low. Now let's attempt to calculate D(S) for the following S:

Extremely complex compound symbol S
First, the label: D(1)=3+1+13+512 (5 primitive letters). That's one way to see it. Another way to see it, is to sum the values of all the primitive letters from the entire wiki article on Camels. That is, D(1)≥14810, without counting external links to the article words and their associated meanings.
D(4) (the Camel figure) has problems. Depending on how we see it, it can be interpreted with different depth. It can be interpreted as a stick figure with 7 appendages, hence one version can have D(4)=7 (regular 7-gon). It can again be interpreted as the entire Wiki entry on Camels, so we already can have D(4)≥14810.
D(2) and D(3) can be interpreted accordingly: D(2)=τ+ο+κ+α+π+ν+ι+σ+μ+α+... (31 primitive letters) and D(3)=a+m+e+r+i+c+a+n+&+d+o+... (22 primitive letters), but if we break down the sentences into their constituent meanings, we end up with huge byte counts for "American" (124076, using only the main link (!)), "Domestic" (??? depending on the country of the smoker) and (tobacco) "blend" (46670), so we have D(2)+D(3)≥170746.
D(5)=3+4 (3 (face) and 4 (base)). Αs long as one avoids the connection with Egyptian "Pyramids" (14253). In the latter case, D(5)=7+14253. So far then, D(5)≥14260. Similar for D(7).
D(6)=3+7+8+9 (3 palms with 7,8,9 leaves each) as long as one avoids the connection with "Palm Trees". In the latter case, D(6)≥27+21826.
D(8)? A bunch of points? So D(8)=30 (that's how many the author can count there), unless one connects the terrain with "desert" (22527).
In addition to the above problems, we also have D(9), D(10) and D(11), which depend on the viewer's subconscious intellect. It is easy to see that certain symbol-shapes lurk there, but are not immediately obvious, because they are interpretation-dependent[2].
Leaving D(12) and D(13) out, we are already at D(S)≥273230. That's a little higher and it's only a lower bound, so here we stop.
For a complex symbol S, it appears as though when r decreases, D also seems to decrease overall. When chaos sets in, D becomes zero, but it is not very clear what D does in between. Intuitively, the sub-symbols which are recognizable become less and less, until D becomes 0, however, certain cases may reveal strong fluctuations which would tend to increase D. For example, for the fundamental symbol S=2, below, it is not absolutely clear that D is always decreasing. For example, the distortion at step n=3 makes it look as if 2 has become something akin to the shadow of a desk-light (??? below):
| D(S)=1 | D(S)=1 | D(S)=1 | D(S)=??? | ... | D(S)=0 |
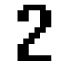 |
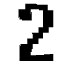 |
 |
 |
... |  |
Some heuristically calculated values for D for the Camel pack are shown below. The relatively high values of D are there because the word "American" is still very recognizable in all pictures except the last:
| D(S)≥273230 | D(S)≥190837 | D(S)≥167938 | D(S)≥124076 | ... | D(S)=0 |
 |
 |
 |
 |
... |  |
Clearly r(S) and D(S) are directly connected with intelligence. Whereas the author sees the shadow of a desk-lamp at n=3 above for the fundamental symbol S=2, another observer may see something different.
Intelligence is a function of recognition and recognition is characterized by a relatively high r(S) being close to 1, while we traditionally think of S's with low (close to zero) r(S) being non-information. In art, the Realist painting school for example, is characterized by very high r's. The higher the r, the more unambiguously S belongs to that school. But that's not the only kind of art. Abstractionist and Surrealistic art for example may be partly characterized by relatively low r's.
A non-zero r(S) virtually guarantees that S contains some minimal information, but it is not at all obvious what this information is or may be[3].
If we denote intelligence by some subjective measurement, such as the IQ, then it appears that we have the following Conjecture:
Depth of Pattern Recognition Conjecture:
If two intelligences A and B have respectively IQ's IQ(A) and IQ(B) with IQ(A)≥IQ(B), and U denotes the universe of symbols, then for all S in U: