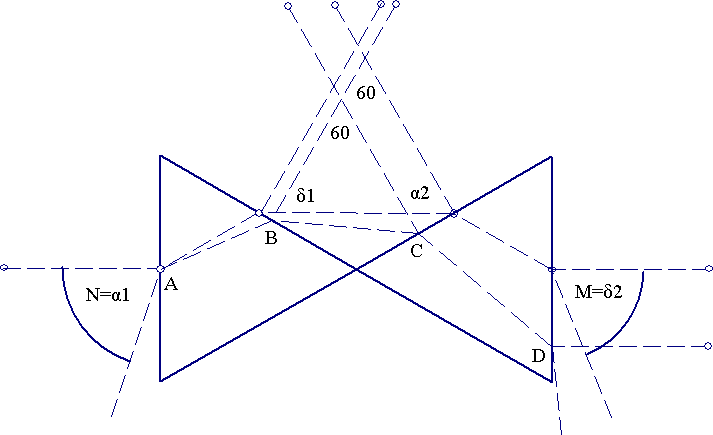

The following calculations assume you have read the analysis on Calculating the deviation angle for a prism.
Note that the first emergence angle at B is given by:
δ1=arcsin{sin(A)*sqrt(nλ2-sin2(α1))-cos(A)*sin(α1)}
(1)
for A=60°, and α1=60°, (1) gives:
δ1=arcsin{sqrt(3/2)*sqrt(nλ2-3/4)-sqrt(3/4)}
=>δ1=arcsin{sqrt(3/2)*(sqrt(nλ2-3/4)-1/2)}
(2)
Now:
60°+δ1+α2=180°=>α2=120°-δ1
(3)
=>α2=120°-arcsin{sqrt(3/2)*sqrt(nλ2-3/4)-sqrt(3/4)}
(4)
Then with incidence angle α2 at C, the emergence angle at D will be:
δ2=arcsin{sqrt(3/2)*sqrt(nλ2-sin2(α2))-sin(α2/2)} (5)
To conclude: First we calculate δ1 using (2), then we find α2 using (3) and finally compute δ2 from (5):
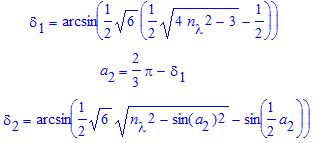
The method above generalizes to n prisms easily, provided we know the angles between them.
For example, we can calculate the spectrum's angular width Δδ2 that way:
| for n=1.77578 | for n=1.71681 |
| δ1=65.446902° | δ1=58.294643° |
| α2=54.553098° | α2=61.705357° |
| δ2=73.569903° | δ2=56.730209° |
=>Δδ2=16.839694°.
Compare this with the ΔE we get from dE/dn=2/cos(arcsin(nD/2)). This formula gives for nD=1.72803, dE/dn=3.9724624 rad, so with a δ(n)=1.77578-1.71681=0.05898 we get ΔE=0.2342958 rad=13.424162°. The difference is understandable, since the formula for dE/dn is valid essentially only for the area of the sodium line D, from where we picked nD=1.72803.
CAUTION:THE WIDTH OF THE SPECTRUM CHANGES AS WE CHANGE THE INCIDENCE ANGLE!
For example: If α1=58°, then:
| for n=1.77578 | for n=1.71681 |
| δ2=79.767447° | δ2=58.593937° |
with a Δδ2=21.17351°
If α1=62°, then:
| for n=1.77578 | for n=1.71681 |
| δ2=69.773023° | δ2=55.198486° |
with a Δδ2=14.574537°
Conclusion: If the incidence angle is <60°, the spectrum is wider. If >60°,it is shorter. (Take this into account later when you measure wavelengths. If you do not get the correct wavelength, it means that your collimator is not at 60° exactly.)