When one observes known objects, one can empirically determine their distance by the viewing angle with which one observes them. In other cases, one can determine their distance by moving one's head slightly, which causes a change of the relative position of their respective image within one's field of vision, which in turn allows one to determine the distance by determining the change of their position. Additionally, distance can also be estimated subconsciously by sensations from the eye's focusing mechanism and particularly by the eyes' muscle movements, whether those are focusing movements or aligning movements.
Excluding eye-muscle adjustment, the above is a lay-man's description for the notion of 'parallax', which is depicted on the following schematics.

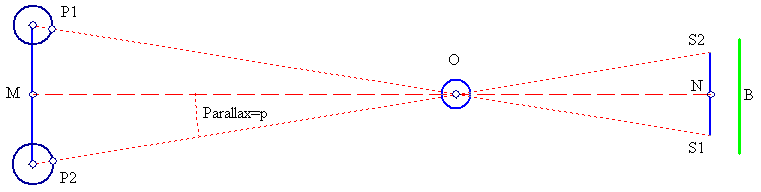
Observer views object O from two different positions P1 and P2. O is closer to the observer than the background B, so the change of position from P1 to P2 forces a change of projection of O to the corresponding positions S1 and S2. Because B is much farther away than O, this change of projected positions is larger for O than for B. Accordingly, the observer perceives a visual change of position of O against B:
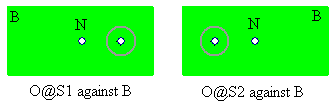
The 'parallax' p then, is half the angular displacement of O against the fixed background B, relative to the observer. The determination of this displacement p, allows for a direct calculation of O's distance using simple trigonometry. This method is also used for stars as well. In the later case, P1 and P2 are taken as antipodal points on Earth's orbit around the Sun, when two measurements are taken, 6 months apart. The parallax shows on the photographic plate as a direct displacement of stars which are close against stars which are farther away.
In two-eyed vision, the two images that reach the retina are not exactly the same because of parallax, and the relative position of various points allows one empirically to judge which points are farther and which closer. This is called 'depth of field'.
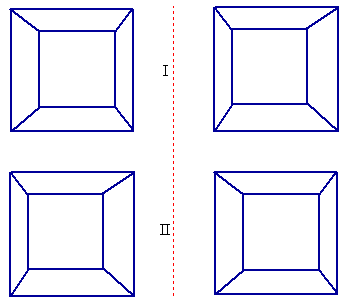
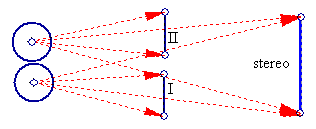
The 'sense' of depth of field can additionally be duplicated with flat pairs of images when each member of the pair possesses exactly those differences in parallax which are required when one views similar real images. For example, in the following schematic, one can simply 'merge' the two images, by using a certain 'cross-eyed' technique. This later, requires some experience.
When the images are successfully 'merged' thus, schematic I will show concave 'depth', while schematic II will show convex 'depth'.
Real stereo photographs can be taken using a regular or digital camera, by using a certain displacement between the photographs, against the same field of view. The stereo sensation is ideal when the displacement between the two photographs is equal to the interpupillary distance, that is, the distance between the pupils of an average human.
The technique is simple: Two photographs are taken, one at position P1, the other at position P2, of object O. The distance between P1 and P2 (which is the distance between the camera between the successive shots) is D(P1,P2)=interpupilary distance=~6.5cm. The greater the distance D, the more intense the stereoscopic sensation when viewing the images merged.
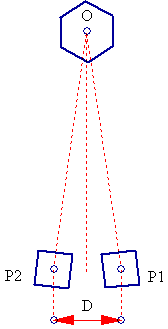
Then the photo from position P1 is placed LEFT and the photo from position P2 is placed RIGHT on the screen and they are merged using a suitable method for stereoscopic viewing. And here are some results:






Another example can be seen on my High Pressure Mercury Lamp Page and an artificial example on Indra's Net of Pearls Page. All the previous examples require some experience to be able to merge the images. The merging happens according to the following figure. Initially each eye views the two images separately. The left eye views image II while the right eye views image I. By 'fusing' the images, the brain forces the two eyes to slightly 'cross-eye' by increasing the angle between the two optical axes, as a result of which the brain now perceives a new image in stereo mode, provided images I and II have the required differences.
When such a conscious method of 'fusing' the two images is not easily achievable, another method is quite popular, that of merging two symmetrical images (around the y-axis) using a mirror.
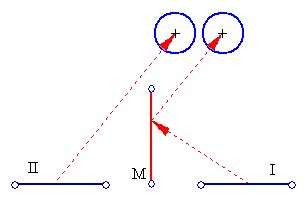
This technique works as follows: One takes two real pictures of a scene with the proper displacement D. Then, one inverts the right image (or left, depending on which image needs to be mirrored) around the y-axis. Both images are then placed side by side. If a mirror M is placed vertically at the location of the red line and the viewer looks at the images so that the left eye views image II, while the right eye views image I reflected through the mirror, then, with a bit of effort when the images merge, the resulting sensation will be stereoscopic. The pairs below have been adjusted so that the right eye views the right image I through the mirror.



Subjectively the mirror method gives a "truer" stereoscopic sensation, primarily because this method is equivalent to the "parallel viewing" method (see below).
The two above methods for stereo photography, succeed for all but one case: Astrophotography. Even when using binoculars which increase D beyond the common interpupillary distance, the distance of the stars is so great that the difference between the two different photographs taken (and thus the parallax) is not sufficient to generate a stereoscopic sensation. However, when the position of locations P1 and P2 is great enough, such as when photographs are taken at antipodal points of the Earth's orbit around the sun, or when parallax is generated artificially, such a sensation can still be generated.


Pseudo-stereographs can also be created from a single image, by applying an appropriate convolution to the original:

Note that all of the above applies to creating cross-eyed stereo photo pairs. There is an alternate technique for fusing stereo pairs together, by viewing each image with a separate eye (parallel viewing). In this case, the images are swapped. For more information on this method, check Dale Gombert's Stereography Pages.
The final method for creating stereoscopic images is of course that which uses red-blue glasses (or some variation therefrom). This method is not covered in this page, because creating stereo images this way is somewhat more involved and more difficult. Interested readers can check this and this link for starters.