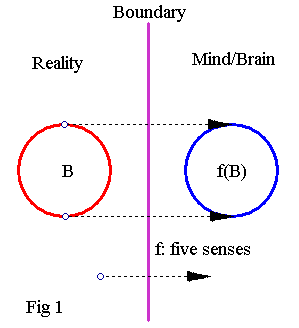
Five senses (f) mapping an object from Reality to Mind/Brain
Can Mathematics help explain what reality is? This article proposes that mathematics is the language which allows information to flow between reality (R) and Mind/Brain (M), and is thus reality's "surveying" mechanism.
So, what is real? Real is what one perceives to be real through one's five senses. And how does one do that? Through an implied "isomorphism" f, between any outside object in R and the corresponding perception in one's mind, which carries information by the five senses into one's brain.

What looks like a real ball B in front of one, gets mapped into a tiny ball f(B) inside one's brain. When B disappears, so does its image f(B). The reverse does not seem to be true: f(B) can disappear (when one closes one's eyes for example) but B does not have to (B can still be witnessed by another observer for example), although there is no way to prove that it does or it does not disappear when f(B) goes.
Certain eastern traditions for example, may conceivably claim that a great thinker might be able to make B disappear, provided he "erases" f(B) in his mind. If this is the case, that killing the perception causes the actual annihilation of the physical object B, then we have a sound basis for explaining the notion of "reality interference", more commonly known as "miracle".
However, the author finds the later highly debatable. Suppose we have two observers Mind1, Mind2, looking at B. The two corresponding perceptions in their minds are f(B) and g(B). Suppose Mind1 is a Zen master and manages to "erase" f(B), while Mind2 is still looking at B. Will g(B) disappear also? The author doesn't know. If this happens, then we have at our disposal a human who can conceivably influence another person's reality.
Being a realist, the author finds such events to be highly unlikely, although again, he is not sure it cannot be done, either.
It seems logical to assume that theoretically the object B and the perception f(B) are different objects. B is a real object after all, whereas f(B) is just a perception (of the object in one's mind). However, if we treat B and f(B) as different objects, chaos ensues and communication becomes impossible. I.e. one person sees (tastes, hears, touches, etc) the ball, while another doesn't. Nonsense.
So most of us treat f(B) as though it is B. Looks like it's the right thing to do (more on this later).
The identification of B with f(B) creates a functional universe with a suitable consensus for shared communication of objects and then by abstraction, of ideas.
When a perceived/conceived idea B' does not have a pre-image through f, then it appears as though it's an object of a certain "fantasy" world, with the word "fantasy" taken in a wider sense, to include abstract notions and objects as well.
Numbers for example, do not seem to have pre-images through f. Neither does the notion of "infinity", or the notion of "perfect Euclidian equilateral triangle". Many if not most mathematical notions seem to be lacking pre-images through f.
Reality seems to be the set of all objects upon which f acts. The body appears to be the set's (reality's) boundary (purple boundaries in all figures). What happens on the boundary of sets almost always raises interesting mathematical questions.
The reason why it appears as though the body C is the boundary, is because the perception of our bodies f(C) is highly incomplete. We certainly cannot "look inside" our bodies, except with the help of medical scopes, and even then the image f(C) would be still lacking, because we cannot possibly see inside every single organ, cell or bone. We can only have a perception of our outer bodies, most likely of our skin, seen as a manifold and not even the whole skin. One can only see a mirror image of one's back, for example. Not the real image of one's back.
Even a skilled pathologist cannot have a complete image f(C) of his entire body, since the knowledge he has about anatomy does not necessarily relate to his own body organs. Contrast the previous with the (almost) complete perception we can have of any external object, animate or inanimate: We can open B up, dissect it, look at its insides, look at what it consists of, and analyze it down to its most basic constituents. We can know B, but not our own body.
Such an analysis is of course in principle possible for other human beings, but not for ourselves. A skilled pathologist can have a complete image f(C) of another person's body, but not his own, provided he has taken the time to dissect every single organ and every crevice. The author seriously doubts that the examinee will survive such an examination, however.
One may claim that one can conceivably enter a CAT scanner and output lengthy details of one's body, but then note that the data from the CAT scanner is not data acquired directly through f. It is not data relayed directly by the five senses. It is data acquired through a different map, a composition of f and h, where h is the CAT scanner map, so the subject here gets complicated. In the same way we don't consider X-ray or ultraviolet images of the sun as data acquired through f we cannot consider the CAT scanner to be operating through the five senses, f.
It is also interesting to note, in view of the above, that a major "correction" of some body parts (some heavy surgery for example), requires a complete shut-down of consciousness (read reality), for the observer (general anesthesia).
The exact delineation of the boundary between reality R and f(R) is not at all clear, but here are some further thoughts:
R and f(R) look like mirror images of themselves. Whatever the exact boundary is, it certainly separates R from that which perceives R, namely the Mind/Brain. f is what carries information from the realm R to the Mind/Brain realm.
Most of us, mainly because of our size relative to the astronomical sizes of R, usually depict the situation a little more humbly, as indicated on the next schematic:
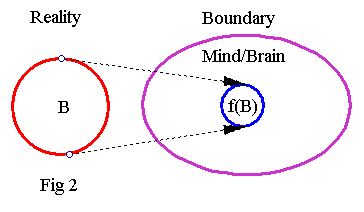
We tend to prefer the later depiction over the first, because our bodies are finite sized, whereas on the first figure the Brain/Mind is implicitly shown as infinite-sized (as the right half plane). The second figure implies that the Mind/Brain realm is (somehow) finite, and R is indicated by some universal external set.
The funny thing however, is that this second schematic can be topologically inverted to give another interesting view:
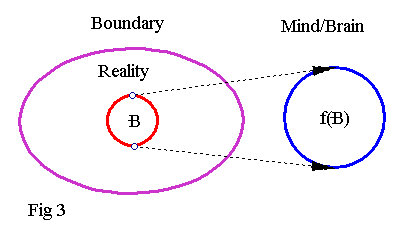
Note that in the third figure, it's the Mind/Brain which is infinite and reality is finite sized. So, is there any real difference between figures 2 and 3? Absolutely none. You can easily consider your Mind/Brain to be the "universe" and reality to be a tiny, finite (albeit astronomically huge relative to our body) part of your mind/brain. Then, all you have there is basically "A" Mind/Brain, contemplating R and examining it through f.
The above is nicely supported by the intuitive fact that anyone's mind, can theoretically expand to any conceivable size, even encompassing the size of the entire universe, provided the person who performs the "expansion" has sufficient knowledge of astronomy and can tangentially understand astronomical sizes.
To further elaborate on a question which was left open in the beginning: Are B and f(B) (or R and f(R) in general) really the "same" thing? It certainly is a useful shortcut to consider R and f(R) to be the same, but unfortunately they are not. A ball B is not the same as the perception f(B) it generates. It certainly looks as though the Mind/Brain makes a quite accurate identification between the two, otherwise we all would be dysfunctional. For example, both R and f(R) appear to be metric spaces with very similar properties: If |f(B) - Boundary| was different than |B - Boundary|, then we would have disorientation problems picking up the ball B, bicycle riding would not work, car driving would send everyone to their grave, etc.
Let B be the moon for example. We first embark on a journey to calculate |f(B) - Boundary|, using Mathematics. The fact that we successfully landed on the moon after our analysis and after Saturn V travelled there, says a lot: That |B - Boundary| = |f(B) - Boundary|. Otherwise, our calculations would have thrown the project off a couple thousand miles. So it appears that mathematics is the language which describes reality's consistency in some sense, through f. If R was inconsistent, then our calculations about it would be too.
And then, what about f's domain? Is it empty before we are born?
Sure looks like it. Can you recall R at the age of 2? 1? When you were a newborn? The author can't. The author hopes the same is true for you. From all appearances, Mind/Brain is unpopulated before a certain age is reached. What does this mean? For this author it means that neither R nor Mind/Brain exist before birth.
Literally speaking, it appears as though we are creating R, as a species. The further we advance in knowledge and numbers, the larger R becomes. Perhaps that's why the universe keeps expanding: To put up with all the minds which have reached all the way out there. Perhaps then, if the population started declining, then R would start contracting, until, when one day there's nobody left, R goes out the window as well. So R seems to be tied to us in one way or another.
The domain of f also appears to be dynamic. The author thinks what makes it dynamic is memory. We cannot continuously keep f(B) for all B in our Minds/Brains. We forget. It appears that the significance of one person forgetting about B, is null. But the author is not sure the significance of everyone forgetting B is trivial. If f provides for a direct correspondence between R and Mind/Brain, then when all forget about B, that is, when f(B) ceases to exist in all minds, it may be that B does indeed disappear from R.
It should also be noted all of the above is a bit simplistic with just one mind. There are billions of minds in our reality. So let us add one more and see if we can gain any additional insight. Here then are two minds/brains, contemplating R, through their respective senses, f and g, according to a classical interpretation which has both minds perceiving the object B and each other:
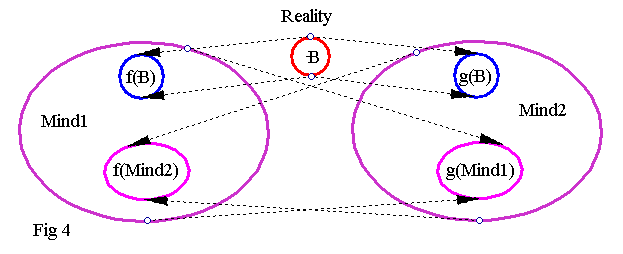
Although the above schematic conforms well to what we know via epistemology and from studying the behavior of other humans, it does not reflect accurately what each one of us perceives individually, because we really cannot know what anybody else but ourselves perceives.
To rectify this, we can identify with one of the above two minds as our own (say Mind1), and we can perform the same topological inversion as the one in figure 3 to the above figure to get a more accurate view of how we view R and the second observer, Mind/Brain2:
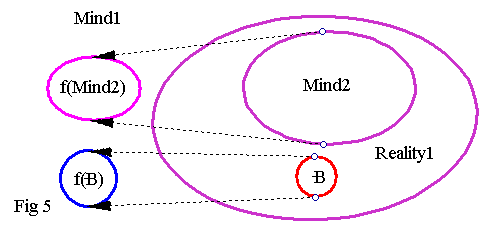
The above is the author (or you, if your mind works similarly to his) looking at reality R and another observer. Several facts are obvious even without the aid of the above figure: The mapping g naturally loses its significance, since no matter how well we can know an external observer, we can never locate g(B) or know exactly how g works for him. We can surgically slice his entire body open, remove every organ, slice and examine his brain, but we won't be able to locate g(B) for any B. From the perspective of Mind1, g(B) does not exist. We can only know that g(B) exists, because Mind/Brain2 assures us that this is the case.
Whether solipsism is true or not, the author doesn't know, but he thinks he knows that one can never know how somebody else perceives reality, so the situation in figure 5 certainly conspires for solipsism.
To avoid the above pitfall, we can try to perform one final topological inversion. That of Mind/Brain2. This situation then, is depicted on the next schematic:
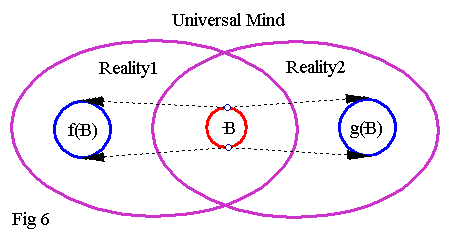
Now things are starting to become clear: There seems to be only one mind, which we can call The Universal Mind, and when there are two observers reality splits into two separate, sometimes intersecting sets. When there are n observers or Minds/Brains, a similar argument shows that reality splits into n sets, all different, since by definition no two humans are identical.
In retrospect, what appears to be happening is The Universal Mind perceiving n different versions of reality simultaneously, with some parts common (when two minds/brains look at the same object for example). This is akin to having n parallel universes (the n reality sets), with the universal mind contemplating all of them independently via each and every observer and the corresponding maps f,g,h,...
Then, what we call "real", looks like the intersection of all these universes. Mathematics appears to be the language that allows f to operate as an isomorphism between the different versions of reality and The Universal Mind. In other words, it is reality's (or mind's, depending on your view) "surveying" mechanism. It takes data from the R's and passes it to Mind/Brain, ultimately populating The Universal Mind with all of reality's different aspects.
The most interesting question of course is, what happens to reality when the boundary (and thus f) disappears altogether.
Nobody knows for sure. Perhaps R disappears, perhaps another map g shows up, which allows the mind to examine other uncharted areas, using a different method. If R goes when f(R) and f go, this is certainly a tremendous waste in the author's opinion. Populating the Mind/Brain via f, takes (literally) a lifetime. So it appears contradictory to this author for nature to create this very complex interplay between R and Mind/Brain, wasting all these resources to achieve this, only to have the whole thing ultimately reduced to null.