Arc discharge sources, such as the High Pressure Mercury Vapor Lamp, the high/low pressure sodium lamp, the fluorescent lamp and the metal halide lamp flicker twice at the mains frequency, that is 100 times/sec at 50 Hz and 120 times/sec at 60 Hz. As the current has usually a sinusoidal shape, the produced arc extinguishes twice in each cycle, giving 50 maxima/sec where the light intensity is maximum and 50 minima/sec where light intensity is off.

Video cameras capture the scenery at a fixed rate per second (fps: frames/sec). Here we show that for certain values of fps, the light flickering for such light sources interferes with the captured scene.

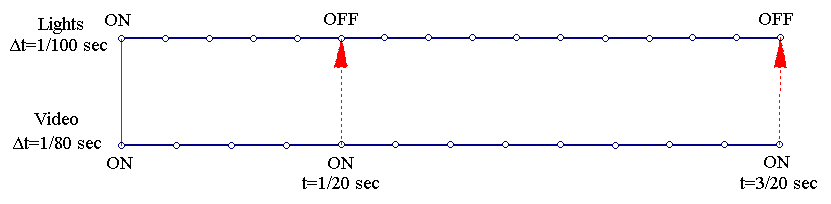
Assume then that the scene is illuminated by high intensity discharge lamps and that the mains frequency is 50 Hz. Assume that the video captures the scenery with a rate of 40 fps. Assume that we start at t=0, with both lamps ON and video ON. Therefore the light intensity becomes maximum at t=k/100 sec, k EVEN and off at k ODD. The video tries to capture the scene at t=j/80 sec, j EVEN and is closed at j ODD.

To determine the times when the video tries to capture the scene while the lights are off, it suffices to solve the equation: (2*k+1)/100=2*j/80.

This equation admits the solution: {j=j, k=5/4*j-1/2}. We need k to be an integer, =>

j=2(mod 4)={2,6,10,14,...}.

j=2(mod 4), =>
k=(5*(4*n+2)-2)/2=(20*n+8)/4=5*n+2, =>
k=2(mod 5)={2,7,12,17,...}.

For n=0 we have a discrepancy at t=1/20 sec:
n=0 => j=2, k=2, and then:
t_light=5/100=1/20 sec
t_video=4/80=1/20 sec

and the video is trying to capture the scene while light intensity is off.

For n=1 we have a discrepancy at t=3/20 sec:
n=1 => j=6, k=7, and then:
t_light=15/100=3/20 sec
t_video=12/80=3/20 sec

and the video is trying again to capture the scene while light intensity is off.

Graphing the times of the two devices, the situation can be visualized as:

It is easy to see now that the times (in secs) when the video tries to capture the scene with the lights off, will be:

t(n)=(2*n+1)/GCD(100,80)=(2*n+1)/2*1/GCD(50,40), n=1,2,3,...,
={1/20, 3/20, 5/20, 7/20,...}

This creates a scene flickering effect which can be seen in this .avi movie (586 KB), in which the author's desk is illuminated by a blended light lamp, which flickers at 50Hz, since it contains a mercury discharge tube.

To avoid this problem when video needs to capture scenery illuminated by light sources which flicker, engineers usually wire subsets of lamps to different phase supplies, in which case no total darkness occurs as some subset of the lamps is always on.

Had the video tried to capture the scene at a rate of 35 fps, things would be very much different. In this case to determine the discrepancies, we need to solve the equation (2*k+1)/100=2*j/70, which admits the solution {j=j, k=10/7*j-1/2}.

It can easily be seen however that k can never be an integer, because 10/7*j-1/2=(20*j-7)/14, and the numerator is always odd, while the denominator is always even. In this case, when the video is ON, there will always be SOME light by the flickering source which illuminates the scene. As such there will be some "scene flickering effect", but its amplitude will be less than in the previous case.

The deeper reason why the first case is solvable while the second is not, is because both equations reduce to:

(2*k+1)/100=2*j/80 <=> 20*j-16*k=8 (1)
(2*k+1)/100=2*j/70 <=> 20*j-14*k=7 (2)

(1) and (2) are classic Diophantine equations. (1) admits a solution because GCD(20,16)=4|8, while (2) does not admit a solution because GCD(20,14)=2 not| 7, which are the exact conditions for the two equations to be solvable in integers.

As an application of the above analysis now, here's another .avi movie (1.9 MB) where at least one kind of modern compact fluorescent lamp (CFL) (Savia 11W 95mA 3000K) does not display visible flicker.

If the CFL pictured above displayed any visible flicker, then the video above should also have displayed flicker, as per the analysis above. But it does not. Hence this particular CFL does not display visible flicker.

Since we know that the source is AC, the above implies that the phosphor persistence is longer than at least a half cycle of the lamp's operation frequency.

Victor Roberts measured below one particular kind of CFL with an oscilloscope:

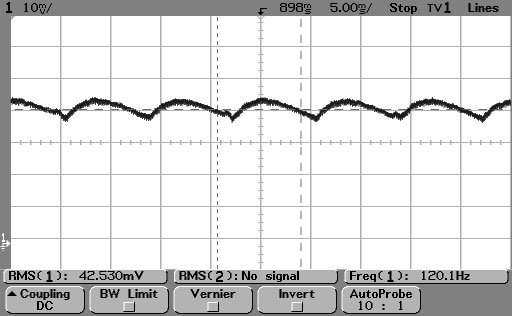
The average output is about 40 mV and the peak-to-peak ripple is about 7 to 8 mV. Hence the modulation amplitude of the light is of the order of 4/40 ~ 10%. Such a modulation is indeed very small and seems to be supporting the analysis above, that it cannot be detected as visible flickering, but other types of CFLs may have wider modulations.