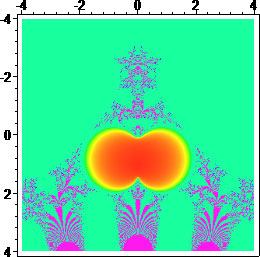
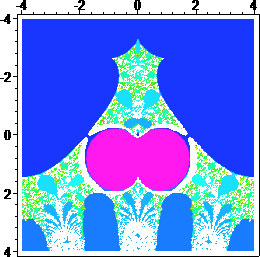
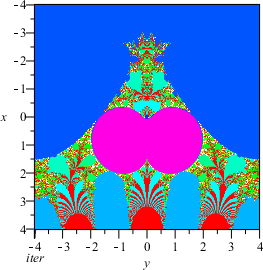
Fig. 1: The infinite tetration fractal by escape and by period, generated with Maple (vs V, 9 and 18).
(The presentation that follows is a light introduction. For more austere results, consult Paper 1).
Having seen the Analytic Continuation of the Hyperpower Function, h(z), it is now instructive to examine the exact association of this function with the resulting fractal which describes the dynamics of the map z|->cz.
The fractal for this map is shown at the end of the Infinite Exponentials article[1]. We include the Maple versions here for completeness:



The orange nephroid bulb on the left figure (and the purple on the second figure), is the area on the complex plane inside which the infinite exponential converges (Shell-Thron region). This area is exactly the image of the complex unit disk D, under the map φ(z)=ez/ez.
Whenever c is inside this area, the limit of the infinite exponential is given by h(c)=W(-log(c))/(-log(c)).
Let's try to visualize the exact basin of attraction of the infinite exponentials which converge. Details in Paper 1 using fixed point iteration show that this basin is exactly the points c for which |φ-1(c)|<1. Since the inverse of φ(z) is -W(-log(z)), we can visualize the basin by looking at the intersection of the plane z=1 and the curve φ-1:
> with(plots):
> W:=LambertW;
> h:=z->W(-log(z))/(-log(z));
> phiinv:=z->-W(-log(z));
> p:=complexplot3d(h(z),z=-2-2*I..2+2*I,numpoints=1000):
> q:=complexplot3d(phiinv(z),z=-2-2*I..2+2*I,numpoints=1000):
> r:=complexplot3d(1,z=-2-2*I..2+2*I,numpoints=1000):
> display({q,r});
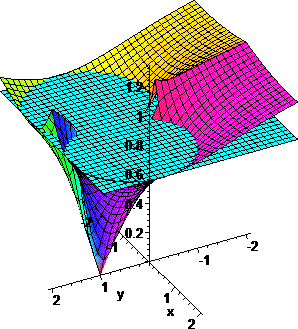
Note the incredible power of the super-attractor, c=1. The nephroid region is the "area of influence" of this point.
Now we can see also the exact limits of the infinite exponential whenever the base
lies inside the basin. For this, we combine the first two plots:
> display({p,q});
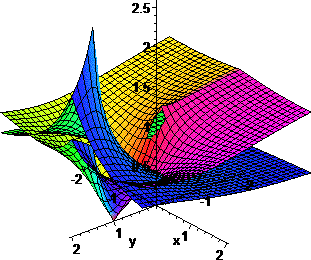
The intersection of the above two curves are the points c on the complex plane such that: |h(c)|=|φ-1(c)|. In other words the points c, with |log(c)| = 1
Next let us visualize all three together:
> display({p,q,r});
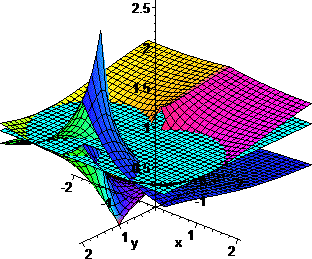
As before, the cyan "sea" is the domain of points c in the complex plane whose corresponding infinite exponential converges. All those points are "pulled" by the super-attractor c=1, towards their limits, h(c), which is the dark blue sheet with the highest peak. The orange and purple sheet are the corresponding multipliers of the points c.
Now let's combine all the plots together, to see the infinite exponential fractal:
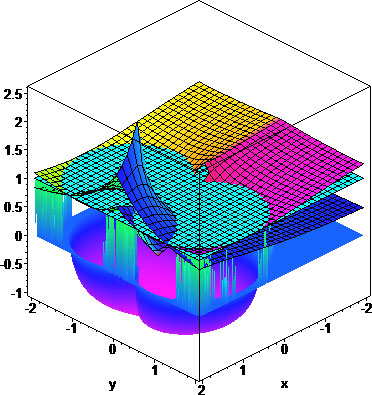
Below the three sheets which are as above, we see a blue/purple sea, which is the complex plane as a function of the number of iterations it takes for the corresponding point's infinite exponential to converge within ε of h(c). The basin of attraction takes the shape of a purple "bowl" which shows which points are attracted by the super-attractor c=1. The sharp spikes are repellers.
We observe that there is a region on the complex plane where |h(c)|>1. Because the curve K={c in C: |h(c)|=1} intersects the nephroid, the corresponding limits h(c) are such that |h(c)|<1 if c belongs to the larger region of the nephroid, while |h(c)|>1 if c belongs to the intersection. The two regions are pictured below:
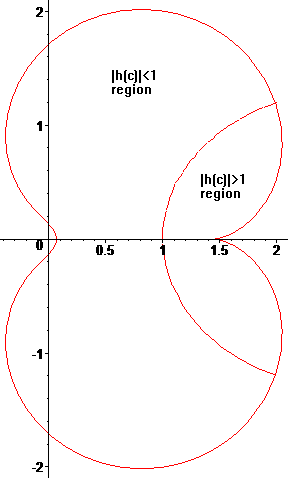
We therefore have the following theorem:
Theorem:
If c in C and ccc... converges, then sup{|ccc...|}=e, and in fact, this value is attained only for c=φ(1)=e1/e.
Proof:
Stare hard at Figures 3, 4 and 5.
In a sense, the peak of h(z) in Figures 3,4 and 5, represents the apotheosis of all efforts using the first 3 fundamental arithmetical operators (addition, multiplication, exponentiation) to produce the ultimate analogy/ratio, under the "tug" of two different super-attractors: 1 and ∞. Points outside the nephroid don't converge but points inside the nephroid arrange themselves according to the absolute value of the corresponding limit of the infinite exponential ccc...=h(c).
Hence the undisputed winner of all such efforts is then the base of the natural logarithm, |h(φ(1))|=e~2.718281828..., which arises as the result of infinite exponentiation of the ideal ratio: φ(1)=e1/e~1.444667861.