n=0
The Cantor Set
Consider the closed interval [0,1]. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; that is, remove the open interval (1/3,2/3). Each successive step of the construction is then essentially the same. Thus, at the second stage, we subdivide each of the remaining two intervals [0,1/3] and [2/3,1] into thirds and remove their interiors (1/9,2/9) and (7/9,8/9), of their middle thirds. We continue the construction for each of the remaining intervals. The general recursion which describes the construction can be summarized as: Cn=Cn-1/3∪(2/3+Cn-1/3).
The subset of [0,1] which remains after infinitely many such operations is called the Cantor set C: thus, if Ck denotes the union of the intervals left at the k-th stage, then C=∩k->∞ Ck.
Since each Ck is closed, it follows that C is closed. Note that Ck consists of 2k closed intervals, each of length 3-k, and that C contains the endpoints of all these intervals. Any point of C belongs to an interval in Ck for all k and is therefore a limit point of the endpoints of the intervals. Thus C is perfect. Finally, since C is covered by the intervals in any Ck, we have |C|e<=2k3-k for each k. =>|C|e=0.
The Cantor Function
If Dk=[0,1]-Ck, then Dk consists of the 2k-1 intervals Ijk (ordered from left to right) removed in the k stages of construction of the Cantor set. Let fk be the continuous function on [0,1] which satisfies:
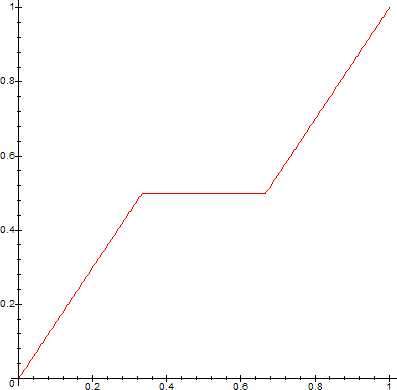
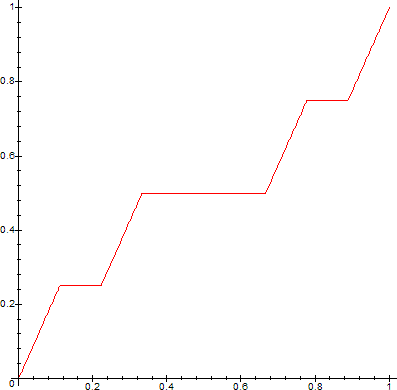
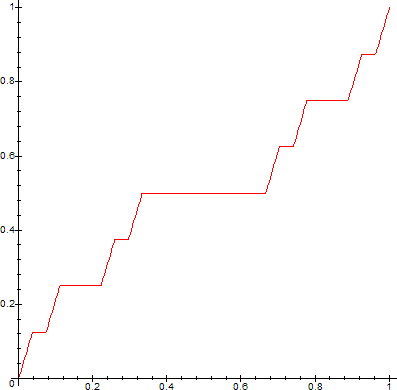
By construction, each fk is monotone increasing, fk+1=fk on Ijk, j=1,2,...2k-1, and |fk-fk+1|<2-k. Hence, ∑(fk-fk+1) converges uniformly on [0,1] and therefore, {fk} converges uniformly on [0,1]. Let f=limk->∞fk. Then f is monotone increasing and continuous on [0,1] and f(0)=0 and f(1)=1. Furthermore, f is constant on every interval removed in constructing C. This f is called the Cantor-Lebesgue function.
Here are graphs of the Cantor Function, produced with the following Maple code:
> CF:=proc(a,b,c,d,n,x)
> option remember;
> if n=0 then
> solve((d-c)/(b-a)=(y-c)/(x-a),y);
> else #n>0
> piecewise(a<=x and
x<=a+1/3*abs(a-b),CF(a,a+1/3*abs(a-b),c,c+1/2*abs(c-d),n-1,x),
b-1/3*abs(a-b)<=x and x<=b,
CF(b-1/3*abs(a-b),b,d-1/2*abs(c-d),d,n-1,x),
c+1/2*abs(c-d));
> fi;
> end:
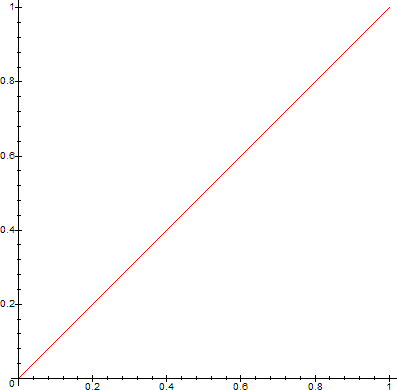
> for n from 0 to 5 do
> plot(CF(0,1,0,1,n,x),x=0..1,numpoints=300);
> od;

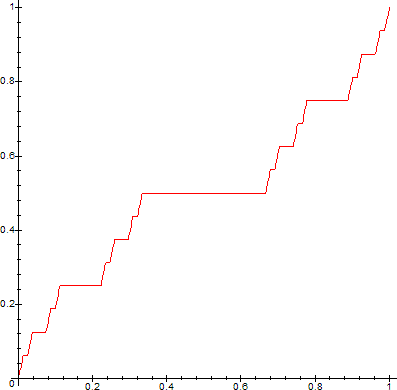
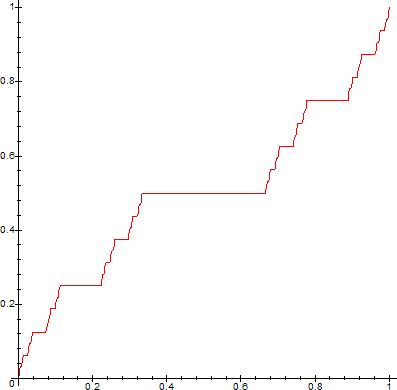
One can now construct some code to test whether values x in the interval [0,1] belong to the Cantor Set. For example, consider this modified Maple code, based on proc CF, above:
> CS:=proc(a,b,n,x)
> option remember;
> if n=0 then
> 1;
> else
> piecewise(a<=x and x<=a+1/3*abs(a-b),CS(a,a+1/3*abs(a-b),n-1,x),
b-1/3*abs(a-b)<=x and x<=b,CS(b-1/3*abs(a-b),b,n-1,x),
0);
> fi;
> end:
CS is the characteristic function of the Cantor Set, hence CS(0,1,n,x)=1 iff x belongs to the set, and 0 iff x does not belong. Let us test some values:
> CS(0,1,10,1/3);
1
Now let us make the investigation a bit more interesting. We know that the Cantor Set contains only ternary decimals consisting entirely of 0's and 2's. Let us check it directly with the Cantor Set characteristic function:
> b3tob10:=proc(L)
> local s;
> s:=sum(L[nops(L)-i+1]*3^(-i),i=1..nops(L));
> end:
> x:=b3tob10([2,0,0,2,0,2,0,0,0,0,0]); # this is 0.000002020023
> CS(0,1,10,x);
1 #bingo! In Cantor Set
> x:=b3tob10([2,2,2,2,2]); # this is 0.222223
> CS(0,1,10,x);
1 #bingo again!
Check a ternary with at least one 1 in its expansion:
> x:=b3tob10([2,2,2,1,2,0,0]); # this is 0.00212223
> CS(0,1,10,x);
0 # not in Cantor Set
Problems
