On 26/7/2006 the author had some gall bladder surgery, where he was forced to undergo general anesthesia. The author carefully monitored his consciousness during the procedure, so here he is attempting to mathematically model the situation.

Assume an "event" is a point in H, or a coordinate quaternion quadruple q=(t,x,y,z), with t,x,y,z>0, similarly to how an event is modelled in physics (so a movie or regular flow of consciousness for example, would be continuous streams of quadruples q(t)=(t, x(t),y(t),z(t)), with no relativistic effects present, so time t is (for our purposes) linear. So we can assume that time and the corresponding streams of events are continuous.

The experience during the shut-down of consciousness was as follows: First, upon the injection of the anesthetic, there was a slight disorientation, which gradually increased. At some point, loss of consciousness occurred at t₁. But the subject (the author) never "experienced" actual loss of consciousness. Instead, the author experienced an awakening into some other forward time t₂, with t₂ = t₁ + 3 hrs, after all the operations were completed.

Using the above notation, and if we assume that the actual moment of unconsciousness occurs at t₁=1 and the moment of awaking occurs at t₂=t₁+3, at loss of consciousness the author was located at q(t₁), with:

q(t₁)= (t₁,x(t₁),y(t₁),z(t₁)) (in the anesthesiologist's room)

and suddenly the author awoke to point q(t₂), with:

q(t₂)=(t₂,x(t₂),y(t₂),z(t₂)) (in the anesthesiologist's room, again).

The author's position was almost identical, so we can assume that x(t₁)=x(t₂), y(t₁)=y(t₂) and z(t₁)=z(t₂).

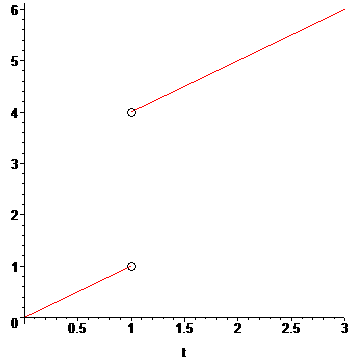
If we describe the time t of uninterrupted normal consciousness as a linear function T(t), the following graph models accurately what happens from the patient's perspective:

Time T(t) as seen by the patient

But the above function is:

T(t)={t, if t<1, t+3, if t>1}.

Converting in terms of the Heaviside step function H,

T(t) = t + 3*H(t-1)

In general, if the moment of unconsciousness occurs at t=t₁ and if the total unconsciousness time is t_Tot=t₂-t₁ then the time of the event stream as experienced from the patient who "goes under" is described by the function:

T(t) = t + t_Tot*H(t-t₁)

Some interesting facts: The patient always measures time along the y-axis. There is a jump discontinuity at t₁=1, where the patient instantly jumps from time t₁=1 hours to t₂=4 hours. The derivative of T(t) is dT/dt=1+t_Tot*δ(t-t₁), with δ being the Dirac delta:

Rate of change of time dT/dt as seen by the patient

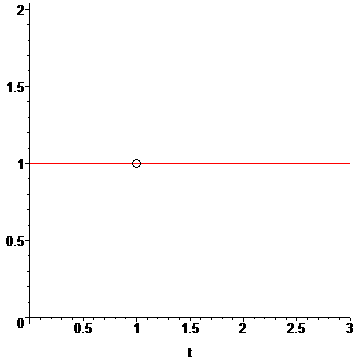
In other words, from the patient's perspective, time passes at a constant rate dT/dt=1 hr/hr (for our function), except exactly at the point t₁=1, when there is a singularity. q(t) for t₁≤t≤t₂ is undefined from the patient's perspective. This is non-existence for a duration of t₂-t₁ hours, so this time is actually lost to the patient, but the patient doesn't experience it, except as an instantaneous singularity which gets lost in the subsequent stream of events.

Now you understand why people are afraid of surgery. Not because of the actual surgery (there is no pain under anesthesia), but because of their encounter with non-existence. Non-existence implies total loss of control and the conscious mind instinctively knows that under total loss of control there might be danger for its survival, hence total anesthesia is something that the mind instinctively avoids.