Having seen how to numerically approximate Lambert's function W, let's also try to numerically approximate its principal branch and branch number 1, using analytic continuation. We will use an example.

Suppose we want to calculate an approximation of W(1+i). We don't know what the value of W is there, but we know some other interesting things. Namely, that W is analytic at 0, hence has a series expansion there.

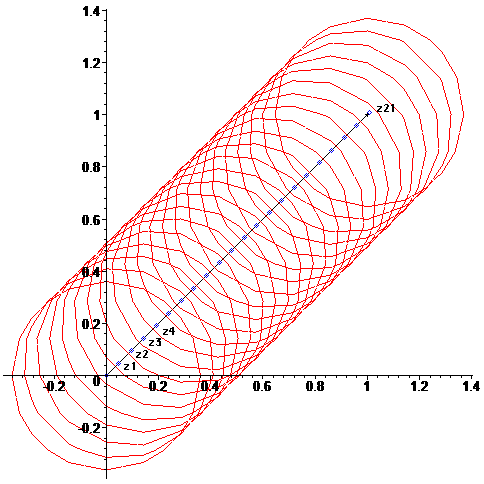
The problem is that this series has a very small radius of convergence, r=1/e and z=1+i is not inside the disk centered at 0 with this radius of convergence. The trick is to consider intersecting disks D_k={z:|z-z_k|<1/e}, which form a connected domain and reach from 0 all the way to 1+i. Here's a picture:

This strategy is simple: We have a series at 0. Use this to calculate W(z₁), where z₁ is a point inside the disk, along the line that connects 0 with 1+i.

If we now are given a formula for the derivative of W(z), we can form a series centered at z₁. Using the last series, we can calculate W(z₂), where z₂ is a point inside the new disk, along the line that connects z₁ with 1+i.

We repeat the above procedure until we reach close to 1+i. When we are close enough, we can use the last series to calculate W(1+i). On the picture, our disk centers are marked as blue diamonds and 1+i is marked with a black cross. Using dr~0.067, the center of the 21-st disk is pretty close to 1+i.

In the Maple code that follows, Maple of course knows the derivative of W(z), but you don't. It is W(z)/(1+W(z))/z. It is also known that W(0)=0. Here's the code:

> r:=exp(-1); #radius of convergence of series for W
> d:=abs(1+I); #distance to 1+i
> epsilon:=0.3;
> dr:=r-epsilon; #inside the disk
> W:=LambertW; #Maple's built in W function
> steps:=ceil(d/dr); #number of circles required

> for k from 0 to steps do
> z[k]:=evalf((k*dr)*exp(I*Pi/4)); #find the points z[k]
> od;

> for k from 0 to steps do
> if k=0 then
> f:=add(limit(diff(W(z),z$n),z=z[k])/n!*(z-z[k])^n,n=1..6); #calculate series around 0
> else
> f:=Wz+add(subs(z=z[k],subs(LambertW(z)=Wz,diff(W(z),z$n)))/n!*(z-z[k])^n,n=1..6);; #calculate series around z[k]
> fi;
> if k < steps then
> Wz:=subs(z=z[k+1],f); #keep the value of Wz we found, because we need it for the next series
> fi;
> od:

> subs(z=1+I,f); #estimated value
.6569660229+.3254515443*I

> evalf(W(1+I)); #actual value
.6569660692+.3254503394*I

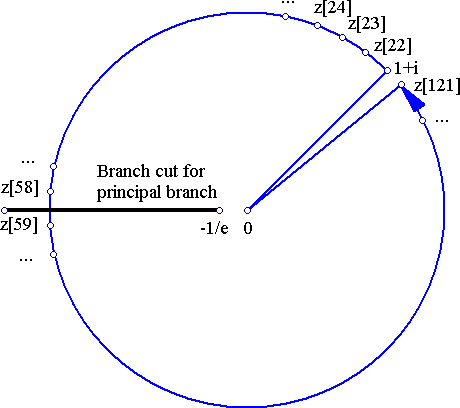
With an error of .1205789244e-5. Pretty good. Now let's try to use the above code to approximate branch 1 of W. Suppose then we want to find W(1,1+i). For this, we construct a path of disk centers z₂₂-z₁₂₁, starting at 1+i, and rotating counterclockwise until we come full circle back (or close) to 1+i. Until we reach the branch cut (z₅₈), we are still on the principal branch. Subsequent points (z₅₉-z₁₂₁) lie on branch 1 of W. See figure below.

We now modify the Maple code to deal with the complete path, from 0 to z₁₂₁. Here it is:

> restart;
> r:=exp(-1); #radius of convergence
>
> d:=abs(1+I); #|1+i|
> epsilon:=0.3;
> dr:=r-epsilon; #offset from center of disk
> W:=LambertW;
> steps:=ceil(d/dr); #number of steps to reach 1+i

> for k from 0 to steps do
> z[k]:=evalf((k*dr)*exp(I*Pi/4)); #construct path z[1]-z[21]
> od:

> r:=abs(z[21]);
> steps:=121-22;

> for k from 0 to steps do
> z[k+22]:=evalf(r*exp(I*((k+1)*Pi/50+Pi/4))); #construct path z[22]-z[121]
> od;

> steps:=121;
> for k from 0 to steps do
> if k=0 then
> f:=add(limit(diff(W(z),z$n),z=z[k])/n!*(z-z[k])^n,n=1..6); #series at 0
> else
> f:=Wz+add(subs(z=z[k],subs(LambertW(z)=Wz,diff(W(z),z$n)))/n!*(z-z[k])^n,n=1..6); #series at z[k]
> fi;
> if k < steps then Wz:=subs(z=z[k+1],f); #approximate value of W at z[k+1]
> #print k+1, value found, actual value and error
> if k < 58 then #we are ready to cross the branch cut! Caution!
> print(k+1,z[k+1],Wz,W(z[k+1]),abs(Wz-W(z[k+1])));
> else
> print(k+1,z[k+1],Wz,W(1,z[k+1]),abs(Wz-W(1,z[k+1])));
> fi;
> fi;
> od;

After running the above code, we get:
> subs(z=1+I,f);
-1.342848857+5.247252283*I

Actual value for W(1,1+i):
> evalf(W(1,1+I));
-1.342848941+5.247249374*I

With an error of:
> evalf(abs(W(1,1+I)-subs(z=1+I,f)));
.2910212535e-5

It should be fairly obvious now, that if we wanted to approximate W(-1,1+i), i.e., W's value of the -1 branch at 1+i, we should work in a similar way, but instead we should be going clockwise, landing again near 1+i.

Hence, by rotating once counterclockwise to 1+i, we reach branch 1 of W, and in general by rotating k times counterclockwise to 1+i, we reach branch k of W, or W(k,1+i). By rotating once clockwise to 1+i, we reach branch -1 of W, and in general by rotating k times clockwise to 1+i, we reach branch -k of W, or W(-k,1+i). In these cases, k is called the winding number of W.

By generalizing the above code and clockwise/counterclockwise strategy, we can compute any value W(k,z), where k is the branch number. Here's the pseudo-code for the full implementation:

procedure W(k:integer; z:complex; steps: integer):complex;
#k: branch number;
#z: Complex number in C;
#steps: for accuracy.
local minSteps,m,n,i,j,p:integer;#minimum number of steps required, counters
zs:complex; #symmetric complex with respect to x-axis
begin
 if Im(z) < 0 then
  conjugate(W(-k,conjugate(z),steps));#call recursively for lower half plane
 else if Im(z) > 0 then
  if Re(z) >= 0 then
   minSteps := ceil(2*|z|*e) + k*ceil(4*Pi*e*|z|); #calculate minimum number of steps required
   if steps < minSteps then
    print(`Minimum number of steps required for accurate results:`,minSteps);
   else
    Construct Disk Centers z[1]-z[m] From 0 to z;
    for i from 0 to m do
     Use f(z[i]) to Construct Series Function f Centered at z[i];
     Store f(z[i+1]);
    end do;
    if k > 0 then
     Construct Disk Centers z[m+1]-z[n] From z Back to z Round the Origin, counterclockwise;
     for j from 1 to k do
      for i from m+1 to n do
       Use f(z[i]) to Construct Series Function f Centered at z[i];
       Store f(z[i+1]);
      end do;
     end do;
    else if k < 0 then
     Construct Disk Centers z[m+1]-z[n] From z Back to z Round the Origin, clockwise;
     for j from 1 to |k| do
      for i from m+1 to n do
       Use f(z[i]) to Construct Series Expansion f Centered at z[i];
       Store f(z[i+1]);
      end do;
     end do;
    end if;
    RETURN(f(z))
   end if;
  else if Re(z) < 0 then
   zs := |x|+y*i;
   minSteps := ceil(2*|z|*e) + ceil(2*(Arg(z)-Arg(zs))*e*|z|) + k*ceil(4*Pi*e*|z|);
   if steps < minSteps then
    print(`Minimum number of steps required for accurate results:`,minSteps);
   else
    Construct Disk Centers z[m+1]-z[n] From z to zs, counterclockwise;
    for i from m+1 to n do
     Use f(z[i]) to Construct Series Expansion f Centered at z[i];
     Store f(z[i+1]);
    end do;
    if k > 0 then
     Construct Disk Centers z[n+1]-z[p] From z Back to z Round the Origin, counterclockwise;
     for j from 1 to k do
      for i from n+1 to p do
       Use f(z[i]) to Construct Series Expansion f Centered at z[i];
       Store f(z[i+1]);
      end do;
     end do;
    else of k < 0 then
     Construct Disk Centers z[n+1]-z[p] From z Back to z Round the Origin, clockwise;
     for j from 1 to |k| do
      for i from n+1 to p do
       Use f(z[i]) to Construct Series Expansion f Centered at z[i];
       Store f(z[i+1]);
      end do;
     end do;
    end if;
    RETURN(f(z));
   end if;
  end if;
 end if;
end;

Implementation details left as an exercise.

For a deeper analysis of the above, consult this answer on math.StackExchange.